Practical Uses for Recursive Javascript

Recursion is one of those classic computer science topics. It’s an interview favorite and often intimidating to beginner programmers. Recursion can provide elegant solutions to extremely complex problems that follow a pattern (e.g. Towers of Hanoi, Fibonacci Numbers, Collatz Conjecture).

How not to use recursion

If used incorrectly, recursion can be dangerous. Not all problems are meant to be solved recursively. Common pitfalls include infinite loops (if you fail to provide termination conditions), memory errors and stack overflows (if the function is deep and memory intensive). All of these issues are avoidable if you follow one rule: don’t use recursion for the sake of using recursion. In addition to the pitfalls above, irresponsible use of recursion can be much slower and more cryptic than iterative solutions.

When to use recursion

Recursion is helpful to know for technical interviews and answering computer science brainteasers, but it has some practical applications, too. The examples below represent valid opportunities to use recursion. However, there are a few points to take into consideration before implementing recursion.

1. Can you implement this more easily with an iterative solution?
2. Does the recursive solution perform better than the iterative one?
3. Is there any possibility of your break condition never evaluating to true?
4. Is there any risk of running out of memory?

Delay Timers

If you want to execute a function multiple times after a set period of time, recursion is a great option. Below is an example:

1
2
3
4
5
6
7
8
9
10
11

var words = ["Hello", " ", "world", "!"];
var n = 0;

function delayLoop() {
    console.log(words[n]);
    if(n++ !== words.length - 1) {
        setTimeout(delayLoop, 1000);
    }
}

delayLoop();

The function above will print successive items from the words array once a second until the end is reached. Here’s how it works:

1. Declare and define the words array and n counter.
2. Declare the delayLoop function.
3. Log the nth element of the words array to the console.
4. Break out of the function if the n counter has reached the end of the words array.
5. Otherwise, wait 1000 milliseconds, then call delayLoop recursively.
6. Invoke delayLoop.

Search Algorithms

Many algorithms lend well to recursion. What if you had to work with a JSON object with a large array of alphabetically sorted properties? Iterating over the entire array from start to finish each time you want to search for an element would be terribly inefficient. Instead, you could use the sorted nature of the array to your advantage using a binary search algorithm.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

function binarySearch( sortedValues, target ){
    function search( low, high ) {
        if ( low > high ) {
            return null;
        }
        if ( sortedValues[low] === target ){
            return low;
        }
        if ( sortedValues[high] === target ){
            return high;
        }
        var middle = Math.floor( ( low + high ) / 2 );
        var middleElement = sortedValues[middle];
        if ( middleElement > target ) {
            return search(low+1, middle);
        } else if ( middleElement < target ) {
            return search(middle, high-1);
        }
        return middle;
    }
    return search(0, sortedValues.length-1);
}

binarySearch([0,1,2,3,4,5,6,7,8,9,10], 4);

On a simplified level, the Binary Search Algorithm takes the following steps:

1. Find the middle element of the given array.
2. Break out of the function if the bottom, middle or top element is your target.
3. If the target is less than the middle element, call the function recursively passing in the left side of the array.
4. If the target is greater than the middle element, call the function recursively passing in the right side of the array.

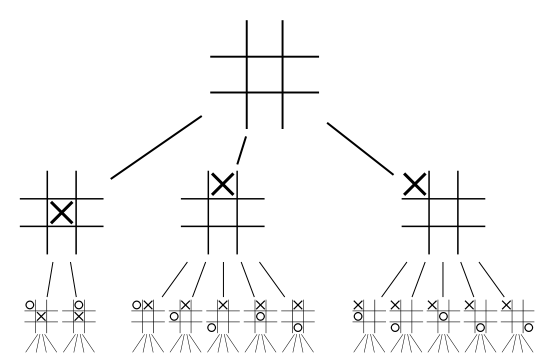
Puzzle Solving

Recursion is an incredibly powerful solution for both solving puzzles and finding the optimized solution for a puzzle. Let’s say you wanted to make an unbeatable version of a board game like Connect Four or Tic-Tac-Toe. An iterative solution could potentially be very complex, as there are a number of factors to consider before making your next move. However, you could determine which move is best through a recursive algorithm that considers all possible future outcomes of the game based on all possible combinations of valid moves by both players. If your game is too complex for an accurate iterative solution and well-defined enough to prevent infinite loops and memory issues, recursion is a powerful tool.